1 概述 
在汽车底盘结构中，有一些受压部件会由于刚度不足而出现失效，从而影响该部件乃至整个系统的正常工作，如转向系统中的转向拉杆，多连杆式悬架中的控制臂，制动操纵机构中的踏板臂等，这些现象属于屈曲问题。 

在工程结构中，压杆稳定性是一种典型的屈曲问题。细长杆件受压时，当压力增加到某一极限值时，压杆将由直线平衡变为曲线平衡，表现出与强度失效全然不同的性质，这个压力的极限值称为临界压力，压杆丧失其直线形状的平衡而过渡为曲线平衡，称为丧失稳定，简称失稳，也称为屈曲。杆件失稳后，压力的微小增加将引起弯曲变形的显著变大，杆件已丧失了承载能力。这是因失稳造成的失效，可以导致整个机器或机构的损坏。但细长压杆失稳时，应力并不一定很高，有时甚至低于比例极限。可见这种形式的失效，并非强度不足，而是稳定性不够。

除了压杆外，其它构件也存在稳定失效问题。例如，圆柱形薄壳在均匀外压作用下，壁内应力变为压应力，则当外压达到临界值时，薄壳的圆形平衡就变为不稳定，会突然变成由虚线表示的长圆形。与此相似，板条或工字梁在最大抗弯刚度平面内弯曲时，会因载荷达到临界值而发生侧向弯曲。薄壳在轴向压力或扭矩作用下，会出现局部折皱。这些都是稳定性问题。 

屈曲分析主要用于估计结构刚性的分歧点，以及结构承担轴向的、膜向、或弯曲变形，解决屈曲前的小变形问题或结构在崩塌前产生非线性问题。结构的屈曲在实际中表现为两种形式：快速通过失稳和分叉失稳。快速通过失稳形式表现为从一个平衡位置快速通过，跳跃到另一个平衡位置，也称为后屈曲。另一种失稳形式常用分叉来描述，失稳出现在两个或多个平衡路径的交点。

2 屈曲分析的一般原理 

对于结构简单的部件，可以采用经典的欧拉公式计算临界载荷，相应的变形可以从截面的惯性矩判断，结构的弯曲变形一定发生于抗弯能力最小的纵向平面内。下面以两端铰支细长压杆为例，对屈曲分析的一般原理进行说明。 

设细长压杆的两端为球铰支座，轴线为直线，压力P与轴线重合。当压力达到临界值时，压杆将由直线平衡形态转变为曲线平衡形态。可以认为，使压杆保持微小弯曲平衡的最小压力即为临界压力。 

选取坐标系如图所示，距原点为x的任意截面的挠度为v，弯矩M的绝对值为Pv。若只取压力P的绝对值，则v为正时，M为负；v为负时，M为正。即M与的符号相反，所以：

M=-Pv

对微小的弯曲变形，挠曲线的近似微分方程为：

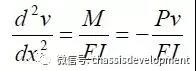
式中的I应是横截面最小的惯性矩。 
对上式进行分析求解，得到临界力为：

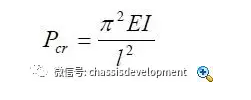
这是两端铰支细长压杆临界力的计算公式，也称为两端铰支压杆的欧拉公式。 
下面以一矩形截面的简支梁为例，应用欧拉公式求解临界载荷。设梁长400，截面宽10mm，高15mm，左端为固定铰支，右端为滑动铰支，在简支梁的右端施加轴向。

 
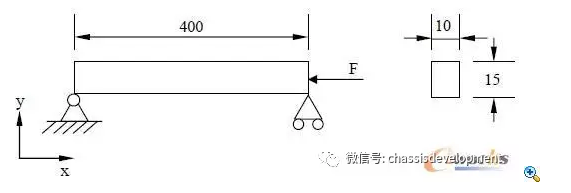
图1 简支梁结构示意图

3 屈曲问题的有限元法求解 

屈曲问题的有限元分析方法大致有两类：一类是通过特征值分析计算屈曲载荷，根据是否考虑非线性因素对屈曲载荷的影响，这类方法又细分为线性屈曲和非线性屈曲分析；另一类是利用结合Newton-Raphson迭代的弧长法来追踪确定加载方向，追踪失稳路径的增量非线性分析方法能有效的分析非线性屈曲和失稳问题。本文只针对第一种方法中的线性屈曲分析进行讨论，这种方法通过提取使线性系统刚度矩阵奇异的特征值来获得结构的临界失稳载荷及失稳模态。 

以节2中的简支梁为例，应用MSC Nastran软件进行线性屈曲分析。有限元分析得到直杆在轴向1000N的压力作用下的屈曲特征值为15.913，从而计算得到该杆能够承受的临界压力为15913N。

 
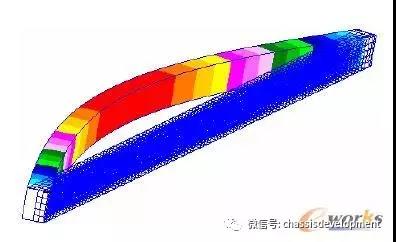
图2 两端铰支杆的变形

对比有限元分析与欧拉公式计算结果不难看出，有限元分析得到的临界压力与欧拉公式计算得到的临界压力基本趋于一致，同时从变形位移图可以看到直杆的一阶特征值对应的为绕Y轴的弯曲，这也进一步说明了杆件的微小弯曲变形一定发生在抗弯能力最小的纵向平面内，欧拉公式中的I为横截面最小的惯性矩。 

4 屈曲分析实例 

汽车底盘中的很多零部件，主要承受轴向拉压或横力弯曲载荷的作用，这些零部件的形状比较复杂，截面特性也随轴线不断变化，因此不能用欧拉公式直接计算。采用有限元法能够比较容易解决此类问题。下面是屈曲分析在汽车底盘结构分析中的一些典型的应用实例。 

4.1 控制臂屈曲分析
在多连杆式独立悬架中，控制臂的受力接近二力杆，受力方向主要为两连接点的直线方向。控制臂的轴向刚度及稳定性直接影响车轮的定位参数，进而影响到整车的操纵性能。因此，对控制臂对行屈曲分析，确定其最大承受的临界压力是非常有必要的。

 
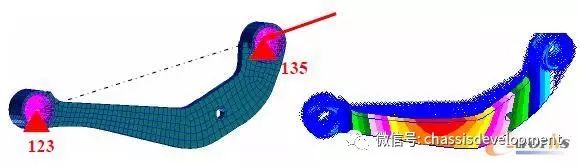
图3 连杆的有限元模型                图4 静载作用下的变形

计算得到控制臂在1000N的轴向力作用下的特征值为48.421，从而能够承受的临界压力为48421N，从振型来看，弯曲变形发生在两个铰支点连线与厚度方向构成的平面内。 

4.2 制动踏板臂 
制动踏板臂的截面通常为矩形截面，为了减小踏板臂的变形，设计中一般采用抗弯刚度大的截面方向来承受操纵力引起的附加弯矩。在操纵力作用下，发生最大弯矩平面内弯曲时，会因载荷达到临界值而发生侧向弯曲。

 
图5 制动踏板臂受力示意图                   图6 静载作用下的变形

某车型的制动踏板臂的结构如图5所示，在踏板端施加操纵方向的作用载荷1000N，计算得到特征值为11.438，则结构发生屈曲的临界载荷为11438N。从图6中可以看到，踏板臂发生屈曲变形为横向弯曲。 

4.3 转向节屈曲分析 
在双横臂式悬架中，通常采用转向节将上、下横臂连接起来，因此上侧支承臂一般设计得比较长，如图7所示。转向节的受力状况比较复杂，转向节上侧支承臂受到三个方向载荷的作用：垂向载荷、纵向载荷和横向载荷，其中垂向载荷最大，在设计中需要重点考察其垂向的承载能力。 

由于转向节中心与轮辋相连，分析中可以将转向节中心固定，在上侧支承臂连接点施加垂向载荷1000N，计算得到结构的特征值为119.97，则临界载荷为119970N，与颠簸工况下的受力情况比较，可以判断结构满足稳定性的要求。

  
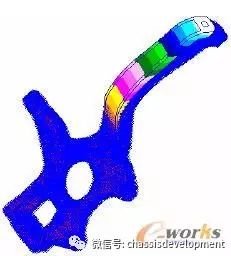
图7 转向节模型              图8 转向节屈曲变形